Introduction of Torsion Formula
In this article we will learn about the derivation and application of the torsion problems. Torsion occurs due to an applied moment. We call the moment torque. So if we try to understand the torsion, we must have the knowledge of torque. What is Torque? In mechanics, Torque is the moment or moment of force or rotational Force or turning effect that tries to twist a member about its longitudinal axis. And in the field of Solid Mechanics, torsion means the twisting or wrenching of a body due to an applied torque.
Assumptions of Torsion Formula
In deriving the torsion formulas the material must follow the assumptions that are proved mathematically and experimentally. The assumptions are given below:
- Circular Sections always remain circular.
- Plane sections always remain plane.
- The material must follow Hooke’s Law. The shear stress must be proportional to the shear strain.
- The material must be homogenous.
- The diameter of that material must rotate by the same angle.
- The stress does not exceed the proportional limit.
Derivation Process of Torsion Formula
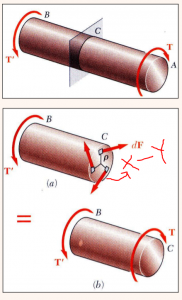
Let us consider a solid circular shaft with radius R which is subjected to a torque T (clockwise) at one end and the other end under the same torque but anticlockwise. Again consider a differential area of section X-Y at a radial distance ρ from the axis of the shaft carries the differential resisting load DF= τ DA.
The angle of radius or angle of twist is φ (Phi)
To satisfy the static equilibrium ΣM= 0 or the applied torque T will be equal to the resisting torque Tr
T= Tr= ∫ρ dF = ∫ρ (τ dA)…………. (Equation 1)
Now, according to the Hooke’s law the shearing stress (τ) is proportional to the shearing strain (γ)
τ= Gγ……….(Equation 2), where G is called modulus of rigidity or shear modulus
[Modulus of rigidity or shear modulus means the measure of the rigidity of a body. It is the numerical ratio of shear stress and shear strain. It is denoted by G. The properties of modulus of rigidity is same as modulus of elasticity.]
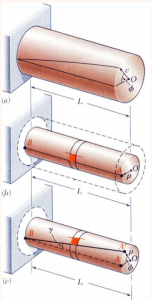
Consider an Interior section of the shaft. From the figure we get,
AA’= ρΦ= Lγ
That’s mean, ρΦ= Lγ
γ= ρΦ/ L……….. (Equation 3)
From equation 2 we get,
τ= GρΦ/ L………. (Equation 4)
Putting the value of τ in equation 1 we get,
T= ∫ ρ GρΦ/ L DA = GΦ/L ∫ρ^2 dA
We know, ∫ ρ^2 dA = J, the polar moment of inertia of the cross section.
[The moment of inertia of an area about an Axis perpendicular to the plane of that area is called polar moment of inertia. It is generally denoted by the symbol J.]

T= GΦ/LJ
Angle of twist, Φ= TL/ JG
[ The angle through which the bar length L will twist is called an angle of Twist. It is denoted by φ (Phi) here
Demonstrations from the derivation of torsion formula
- τ= Tρ/J and τ max= Tc/J, where c is the radius
- γ= cΦ/ L, where c is the radius
- as for a solid shaft, the value of J= πr^4/2, so the value of Max. τ= 2T/πr^3
- as for a hollow shaft, the value of J= π/2 (R^4-r^4), so the value of Max. τ= 2TR/π(R^4-r^4)
Problem: Shaft BC is Hollow with inner and Outer diameters of 90 mm and 120 mm respectively. Shafts AB and CD are solid of diameter,d. For the loading shown determine (a) the maximum and minimum shearing stress in shaft BC (b) the required diameter D of shaft AB and CD if the allowable shearing stress in these shafts is 65 Mpa.

Solution:
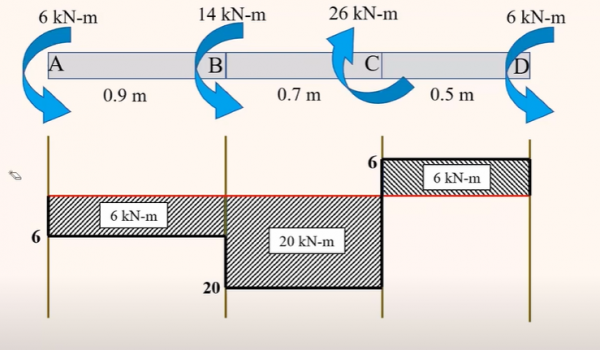
(a)
J= π/2 (R^4-r^4)= π/2 (0.06^4-0.045^4)
= 13.92* 10^-6 m^4
Max. τ= (20*10^3*0.06)/ 13.92* 10^-6= 86.21 Mpa
(Min. τ/ Max. τ)= 0.045/ 0.06
Min. τ= 0.045* 86.21/ 0.06= 64.7 Mpa
(b)
Max. τ= T(AB)*c/J = T(CD)*c/J
65*10^6 pa= (6*10^3*c)/(π/2 c^4)
c= 0.039 m= 38.9 mm
Diameter, d = 2c= 77.8 mm
Reference- BYJU’S
Previous post by the author- Social Contract Theory 1




