What is the Deflection of beams?
The deflection of beams is considered as one of the most important aspects in designing beams. It can be determined by various methods like double integration method, area moment method, conjugate beam method, and the method of superposition. In this article, we will broadly discuss the Deflection of beams
Double- integration method of deflection of beams
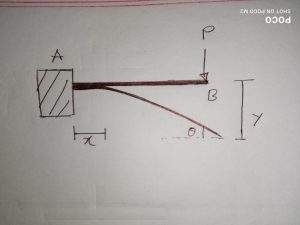
Let us consider a cantilever beam. The fixed point of the beam is A and at point B we will apply load, P. Then the beam will deflect and will form an elastic curve. From the figure, we get the slope,
tanθ = dy/dx.
That’s mean, θ= dy/dx………..(Equation1)
And dθ/dx = d2y/dx2……….. (Equation 2) d2y/dx2
Now from the derivation of the flexural formula, we get the moment-curvature equation
1/R=M/EI……… (Equation 3), where EI is called the flexural rigidity of the beam (how much the beam will resist bending)
From elementary calculus the curvature of a plane at a point Q (x,y) is
1/R= (d2y/dx2 )/ [1+(dy/dx)2]3/2 ………..(Equation 4)
As we have considered the deflection of beams forms an elastic curve, the value of dy/dx is so small. And so the value of (dy/dx)^2 is very very small. so after neglecting the value of (dy/dx)^2 we get,
1/R= d2y/dx2 ………..(Equation 5)
And so, from equation 3 and equation 5,
d2y/dx2= M/EI
EI d2y/dx2= M ………..(Equation 6)
This equation is known as the differential equation of the elastic curve of a beam where EI is constant along the beam. we can get the equation of deflection of beams by integrating this equation twice. Every time we will get a constant after completing the integration.
After the first integration, EI dy/dx= ∫ M dx+ c1
Again, by integrating, EI y= ∫ ∫ Mdx dx + c1x+ c2
Calculating the values of the constants c1 and c2 from the equation of deflection of beams
The constants c1 and c2 are determined using boundary conditions. We consider three types of beams in calculating the values of constants. They are-1. The simply supported beam 2. The overhanging beam 3. The cantilever beam. In the first two types, there is hinge support. And so the beams can rotate freely. But the cantilever beam can not rotate freely. So the procedures of determining the constants are different.
For Cantilever beam
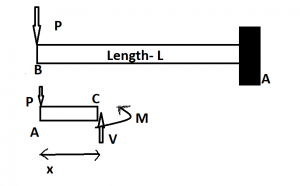
Using a free body diagram we get the moment,
M=-Px…….. (Equation a)
Using the value of M in the equation 6 we get,
EI d2y/dx2= -Px …….. (Equation b)
By integrating, we obtain,
EI dy/dx= -1/2 Px^2+ c1…………. …….. (Equation c)
At the fixed point A, x= L, y= 0, dy/dx= 0, θ = 0.
By using the values, from the equation c we get,
0= -1/2 PL^2 + c1
c1= ½ PL^2………… …….. (Equation d)
Now from the equation c, we get,
EI dy/dx= -1/2 Px^2+ ½ PL^2…………. …….. (Equation e)
By integration, EI y= 1/6 Px^3+ ½ PL^2 x+ c2……….. …….. (Equation f)
But at A, we have x= L, y= 0, dy/dx= 0, θ = 0.
By substituting the values, c2= -1/3 PL^3…………… (Equation g)
This is how we get the values of the constant c1 and c2 for a cantilever beam
For Simply supported and overhanging beam
To apply the double integration method in the simply supported beam and overhanging beam we need to split the beams into some sections. Then we have to individually calculate the moment in the section.
At first let us consider a very simple configuration of a simply supported beam. It is given in the figure.
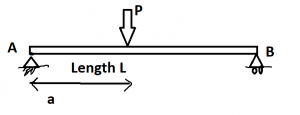
From the figure b, at the left side of the applied force [only the reaction force]
Summation M= 0
⇨RAx- Mx= 0
⇨ RA= Mx
from the figure c, at the right side of the applied force [Reaction force+applied force]
⇨ RA x- P (x-a)- Mx =0
⇨ Mx = RA x- P (x-a)
But,
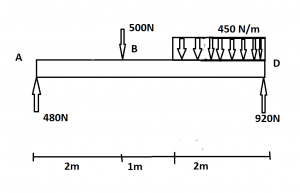
when a uniform load is applied on the beam just like the figure then the moment equation are
M AB= 480x N.m
M BC= [480 x- 500 (x-2)] N.m
M CD= [480 x- 500 (x-2)- 450*(x-3)*(x-3)/2]
But this procedure is only valid if the uniform distributed load extends all the way to the end of the beam. If it is not then we have to adjust the equation by balancing.
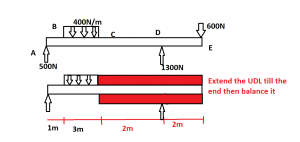
Here the uniformly distributed load is not till the end of the beam. So after balancing we get,
M AB = 500 x
M BC = 500x – 400* (x-1)* (x-1)/2
M CD = 500x – 400* (x-1)* (x-1)/2 + – 400* (x-4)* (x-4)/2
M DE = 500x – 400* (x-1)* (x-1)/2 + – 400* (x-4)* (x-4)/2+ 1300 * (x-6)
Reference- Wikipedia
Previous post from the author- The Best 1 Derivation of Torsion Formula




